Limit of validity. As Constantino Tsallis himself describes [IV.i], it was during a coffee brake of a workshop, held in 1985 at the Instituto de Física (Universidad Nacional Autónoma de México) in Mexico City, that he observed at a distance a professor talking to an attending student and pointing out at the board the combination of symbols p to the power q typical of the description of geometric multifractal sets. This made him consider a generalization of the familiar entropy expression in statistical mechanics and information theory. To his surprise, and to many others, the generalized expression preserves to a large extent the mathematical structure of the ordinary theory, or where there appear variants these are obtained without much difficulty.
The initial publication of these developments [76] produced an enthusiastic response that translated into many studies and related publications [58], but also to skepticism [75, 76]. Over the years this issue has developed into an evolving topic, under the names of nonextensive statistical mechanics or q-statistics [58] [III.iv.10], which carries with it an exploration of the fundamental basis of this branch of physics. It carries the implication, if appropriate pertinent, of a limit of validity of the firmly established Boltzmann-Gibbs (BG) equilibrium statistical mechanics. Well-founded answers and thorough understanding have been awaited up to the present time while a large body of published studies has been assembled and it is still growing.
We have developed an interest and have carried out research in this subject since the early stages and up to now. Our motivation has been two fold: The quest and substantiation of concrete instances in which the BG theory fails and the alternative theory is seen to be applicable. And relatedly, the understanding of the breakdown, if it is indeed the case, of the BG formalism, the underlying cause of the occurrence of a limit of validity of an otherwise unbeaten physical theory.
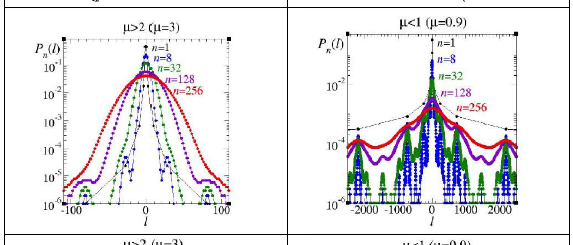
Our early studies referred to our generalization of the Weierstrass random walks [I.iv.1, I.iv.5] to show the connection between the RG technique and entropy optimization. A setting that we used to show the relationship of these walks with the anomalous dimension in criticality and found of a role for the q-index of q-statistics [I.iv.1]. Then we made use of the same random walks to discuss the transit from ordinary to anomalous diffusion [I.iv.2] with reference also to transport in porous media [I.iv.3].
Our main effort, spanning two decades, to understand the implications of a generalized statistical mechanics has been focused on the field of nonlinear dynamics, specifically the transitions to chaos in dissipative systems. This choice was and is motivated by the fact that the chaotic attractors present in these systems possesses the fundamental properties of BG statistical mechanics: ergodicity and mixing, and that these two essentials breakdown at the borderline situation, the transition attractors from chaotic to regular behavior.
The additional feature of relative simplicity of (precise, exact) access to their properties makes low-dimensional mathematical models desirable numerical laboratories for this purpose. The entire contents of Part III of this research report, its twelve sections, have produced concrete advances related to the q-statistics issue, at the same time these studies have revealed the areas in condensed matter physics and in complex systems where the generalized statistical-mechanical formalism is applicable. See the review articles in Refs. [52, 53, 54].
For an earlier account of the initial stages of q-statistics and of our motivations to participate in the development of this subject see Ref. [IV.i] But it was only very recently [IV.ii] that several apparently separate pieces of research came together to create an important advance in the understanding of how the limit of validity of the BG theory arises and in what way it is replaced by, precisely, q-statistics. This fusion or amalgamation requires first a change in perspective when considering the familiar phase space variable x in one-dimensional nonlinear iterated maps f (x). Instead of seeing such maps as systems composed of only one degree of freedom, they can be seen to represent systems with many, infinite, degrees of freedom, when described thermodynamically through a macroscopically observable variable like the energy or the magnetization, the map variable x.
In other words, from this viewpoint the map includes already a (generalized) thermodynamic quantity, the result of the familiar average of (microscopic) configurations in statistical mechanics that results in (macroscopic) observables. Then the next step is to consider not only stationary (equilibrium) states but also processes that lead to these final states. We resort to the rate equations (that we have referred to in Section II.iii) for the description of the kinetics of phase change in condensed matter physics, such as the dissipative Landau-Ginzburg equation [25, 30] [II.iii.1] discussed here in Part II. We focus on the differential equation variable, the driving force of the equation, and its Lyapunov function [77][II.iii.1].
After this we show that the discrete time version of the Landau-Ginzburg equation is a dissipative nonlinear iterated map f (x) and that the general choice of the Renormalization Group (RG) fixed-point maps for the three known routes to chaos capture a wide range of possible applications (including those described in the twelve sections of Part III). In addition to all this we demonstrate that the RG fixed point maps and all of their trajectories have analytical closed q-exponential expressions. Technically, the results of this approach are: i) The q-exponential function as the fabric of the RG fixed-point maps for the three routes to chaos. ii) Its inverse function the q-logarithm, identified as the Tsallis entropy expression, that, significantly, turns out to be the Lyapunov function of the discrete time Landau equation.
As for a brief explanation of the limit of validity of ordinary statistical mechanics and the subsequent incidence of Tsallis statistics: These are a consequence of the effect of the RG fixed-point maps attractors in reducing drastically the initial phase space, or in terms of the phenomena modeled by them, in a severe hindrance to access initially available configurations. See Ref. [IV.ii] for a detailed analysis and explanation.