PRESENTATION
A Half-Century Research Footpath in Statistical Physics
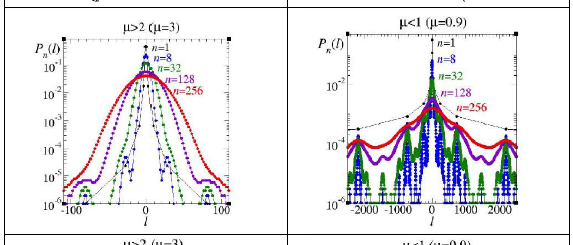
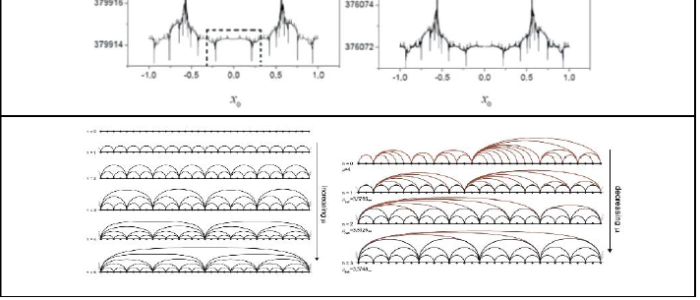
We give an abridged account of a continued string of studies in condensed matter physics and in complex systems that span five decades. We provide links to access abstracts and full texts of a selected list of publications. The studies were carried out within a framework of methods and models, some developed in situ, of stochastic processes, statistical mechanics and nonlinear dynamics. The topics, techniques and outcomes reflect evolving interests of the community but also show a particular character that privileges the use of analogies or unusual viewpoints that unite the studies in distinctive ways. We place the studies into three collections according to the main underlying approach: stochastic processes, density functional theory, and nonlinear dynamics. In the first group we include the following: i) Random walks for fluid correlations. ii) Random walks for electronic band structures. iii) Trapping of multiple walkers. iv) Renormalization group and entropy for Weierstrass walks. v) Statistical-mechanical analogy for renewal pro- cesses. vi) Phase transitions along time in correlated renewal processes. In the second group: i) Density functionals and Widom’s particle insertion method. ii) Liquid to solid transitions in hard-core model systems. iii) Nucleation and spinodal decomposition. iv) Global wetting phase diagrams. v) Lattice models for complex fluids. vi) Anomalous micellar solution criticality. vii) Complex fluids under confinement. viii) Density func- tionals for curved interfaces. ix) Curvature interfacial transitions. x) Line tension and wetting. xi) Classical and quantum mechanical analogs built in density functional the- ory. xii) Phase behavior and pairing mechanism for two-dimensional superconductors. In the third group: i) Critical fluctuations and the route out of chaos. ii) Glassy dynamics at the noise-perturbed onset of chaos. iii) Localization transition as a bifurcation. iv) Pesin identity at the Feigenbaum attractor. v) Renormalization group for chaotic attrac- tors. vi) Self-organization along the period-doubling cascade. vii) Universality classes of rank distributions. viii) Complex network view of the routes to chaos. ix) Chaos in discrete time game theory. x) Equivalence of paradigms (edge of chaos and criticality). xi) Allometry in biology and human activities. xii) Nested systems. We discuss the body of knowledge created by these research lines in relation to theoretical foundations and spread of subjects. We indicate unsuspected connections underlying different aspects of these investigations and also point out both natural and unanticipated perspectives for future developments. Finally, we refer to our most important and recent contribution: An answer with a firm basis to the long standing question about the limit of validity of ordinary statistical mechanics and the pertinence of Tsallis statistics.