Onset of chaos. A chance communication between Robert May and James Yorke in1973 [47] led to the comprehension of the bifurcation diagram of the quadratic map, perhapsnowadays the better-known picture symbolizing nonlinear dynamics. This diagram illustratesthe families of attractors or stable solutions for this difference equation and was first put together by linking the works of May [48] and Yorke and Tien-Yien-Li [49]. Not long after this, Feigengaum contributed [50, 51] to the full understanding of the universal scaling properties at the period-doubling accumulation point, the borderline between regular and irregular behaviors, the transition in and out of chaos.
Twenty-odd years ago we began, then increased and more recently consolidated, a linked set of research lines dedicated to the investigation of complex systems. This set rests on independent, original and rigorous developments on the transitions to chaos in dissipative nonlinear systems of low dimensionality, among which the quadratic map has been the most frequently used. Our investigations are based on two groups of properties we obtained and developed into effective research tools: the dynamics inside and the dynamics towards the attractors that represent the transitions to chaos. Based on this knowledge, studies on core problems of complex systems have been carried out. In the physics of condensed matter we have obtained results in problems of difficult treatment: glassy dynamics, localization and critical fluctuations. In complex systems we have achieved central results for evolutionary dynamics, ranked data distributions (Zipf and Benford laws), and on the rationalization and (needed) statistical-mechanical justification of the phenomenon of self-organization. Recently we demonstrated the equivalence of paradigms in this field, edge of chaos and criticality.
Our motivation to examine the transitions to chaos displayed by prototypical nonlinear iterated maps, such as the logistic and circle maps, originated from the goal to understand the possible existence of a limit of validity of the ordinary Boltzmann-Gibbs statistical mechanics and the conceivable appropriateness of the alternative entropy expression proposed by Tsallis[IV.ii.1]. The failure of both ergodic and mixing properties at these transitions, valid for their neighboring chaotic attractors pointed at a feasible numerical laboratory in which to explore these issues. As a consequence of this all the studies described in this Part III contain results related to our quest of comprehending the so-called q-statistics.
With regards to complex condensed matter physics problems we mention the following: The joint use of density functional theory (for inhomogeneous systems) and the renormalization group fixed-point map (for the tangent bifurcation) to deliver a space-time description for the dominant fluctuation at a critical point. The bifurcation gap induced by addition of external noise, that removes the period-doubling and chaotic-band-splitting accumulation points, was shown to appear as a crossover phenomenon along time evolution at the onset of chaos. We found that before the crossover the dynamics is analogous to glassy dynamics in molecular systems. In addition a vital recursion relation for size growth of a basic wave scattering model was recognized as a nonlinear iteration map with a bifurcation diagram where tangent bifurcations separate periodic (insulating) and chaotic (conducting) attractors.
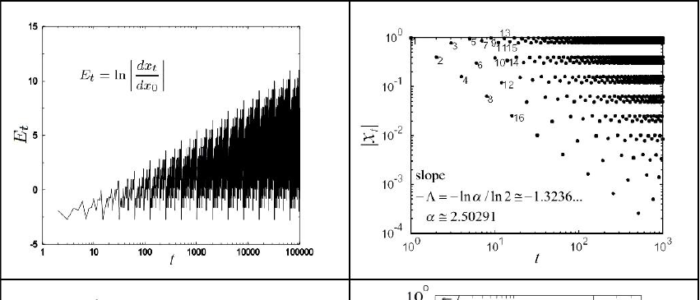
Amongst specific advances in nonlinear dynamics we make reference to: A central quantity in nonlinear dynamics, the sensitivity to initial conditions, was determined explicitly for the pitchfork and tangent bifurcations as well as for the period doubling and the golden ratio quasiperiodic transitions to chaos, all of which display anomalous properties while their Lyapunov exponent vanishes. The distributions for sums of successive positions of trajectories, as in random walks, for families of chaotic attractors of the quadratic map were found to conform to a renormalization group scheme such that its trivial fixed point matches the central limit theorem. From the start, the property that summarized our calculations for the dynamics towards the periodic attractors of the quadratic map resembled formally that of a partition function. Continued work supported this interpretation and finally a model for self-organization materialized.
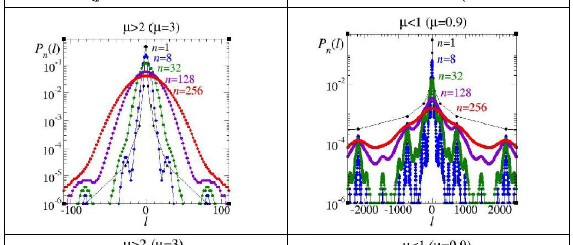
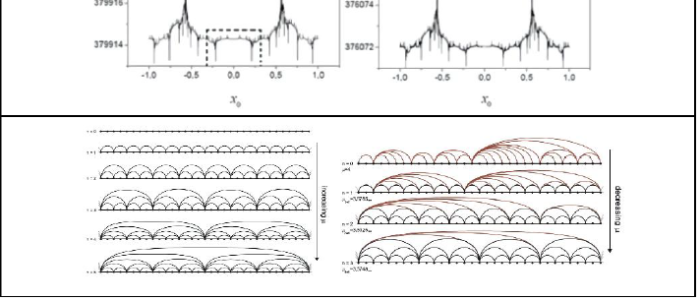
With reference to contributions to the general understanding of complex systems we annotate: The initial consideration of the discrete-time version of the replicator equation of established models of evolutionary game theory lead straightway to novel bifurcation diagrams and valuable coupled-map models. The transformation of iterated map trajectories into (Horizontal Visibility) networks opened the possibility of reevaluating the link of the renormalization group technique with entropy optimization, and likewise the generalization of the Pesin theorem at the transitions to chaos. The size-rank distribution of all kinds of numerical data, including Zipf’s law, were seen to be obtainable from nonlinear maps close to a tangent bifurcation, such that data samples are reproduced by their trajectories.
For reviews that contain descriptions of these developments see [52, 53, 54]