Inhomogeneous states. Benjamin Widom considered the configurational (statistical mechanical) effect of the addition of a degree of freedom in an equilibrium system already composed of many of them [17]. He found a route, amenable for the study of inhomogeneous systems [18], to evaluate the equation of state for the chemical potential. We found that Widom’s expression is the Euler-Lagrange equation (the vanishing of the first variation) associated with the corresponding free energy density functional. This identification opened many possible studies of equilibrium states, particularly non-uniform ones, like spatially ordered states, e.g., solids, phase coexistence, surfaces, etc. The additional degree of freedom could be a particle, a spin flip, different types of molecules in a mixture, even a step in a walk, an event in a renewal process, and so on.
Through this statistical-mechanical route we obtained descriptions for: liquid to solid transitions in hard core systems, like hard spheres; interfacial structures for the known (van derWaals) types of binary mixtures; kinetics of phase change, growth via interface advance, nucleation and spinodal decomposition. We determined global phase diagrams for wetting transitions at fluid mixture interfaces, and developed lattice models for micellar solutions, block copolymers and microemulsions. We also analyzed the modifications undergone by surface phase transitions through capillary confinement, including nematics and quiral molecule mixtures. In relation to wetting transitions we explored the features of a different type of inhomogeneity, that when interfaces meet and produces a line of tension. Finally, a particularly extensive set of studies contain the global phase diagram for the antiferromagnetic (mean field) spin-1 model, that complements the rich phase behavior of the (mean field) ferromagnetic case studied previously by Griffiths.
Another formal advance we carried out within density functional theory was to extend the customary approach to study a planar interface to a full three-dimensional inhomogeneity. This effort yielded statistical mechanical expressions for the rigidities of curved interfaces that are now added to their counterpart for the surface tension, the so-called Triezenberg-Zwanzig expression derived a couple of decades earlier. Furthermore, this development made contact with and gave microscopic support to the phenomenological free energy expression of Helfrich, a basic starting expression for the study of microemulsions. Also we extended our approach to the already mentioned line tension and in general to the stress tensor associated with deformations descriptive of more general inhomogeneous systems.
This second development led to an additional set of more specific results, amongst them
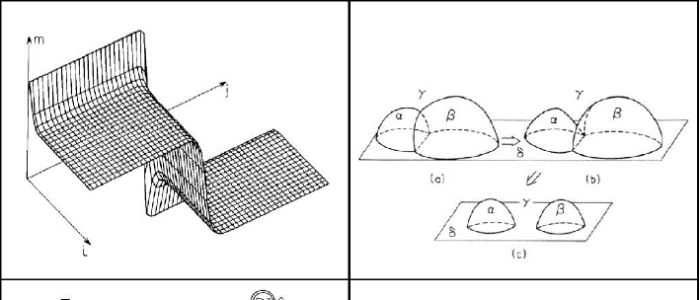
the suggestion of a new kind of two-dimensional phase transitions, mediated by the interfacial curvatures of interfaces. For instance, the transformation of a singly-connected surface into either multiply-disconnected or multiply-connected surfaces. The interfacial rigidity appears as a relevant field in a free energy quantified via the genus of the surface and the Gauss-Bonnet theorem. It indicates a possible mechanism for the inception of micellar solutions or bicontinuous microemulsions from saturated amphiphile monolayers. Another case arises when considering the arrest, mediated by the presence of amphiphiles of a phase separation process, such as nucleation or spinodal decomposition. This stoppage offers another view of microemulsion formation. Finally, an extension of the capillary wave model for interfacial curvature fluctuations followed too.
A third stage was to focus on the basic procedure of the density functional approach. This consists of two steps, the vanishing of first variation of the free energy functional and the calculation of the sign of its second variation fixed by the solution of the 1st condition. The former locates the stationary solutions while the latter discriminates between maxima, minima or inflexion-point solutions. As it had been earlier noticed by Widom [19], the 1st condition is equivalent to a classical-mechanical particle problem, while the 2nd condition can be expressed as a quantum-mechanical particle eigenfunction problem. In our work these mechanical analogies were used to identify statistical-mechanical instabilities in simple liquids: the irrelevance for the position of the Gibbs dividing surface for planar interfaces, the Raleigh breakup of cylindrical jets, and the Laplace equation at the onset of spherical droplet nucleation. Other more complex behaviors were obtained for complex fluids containing amphiphiles.
Additionaly, we made use of our statistical-mechanical know-how in relation to the discovery of High Tc superconductivity and the frenzy of research activity that took place after this. From the body of accumulated experimental evidence a detailed picture was put together of a characteristic phase diagram for these materials. A rich assembly of properties that involves structural phase transitions driven by small variations of impurities or vacancies, that in turn triggers other phase changes, from antiferromagnetic to conducting, to superconducting phases. And to add interest, the mystery of the pairing mechanism. We contributed with a plausible complete description for the different phase behaviors and a novel proposition for a pairing mechanism based on the two-dimensional topological Kosterlitz-Thouless class of phase transitions [20].
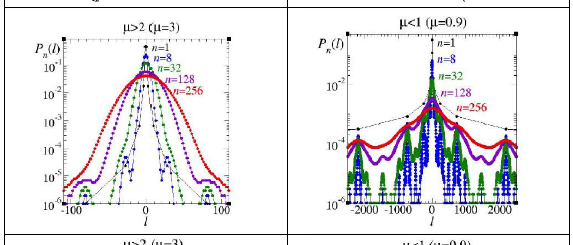
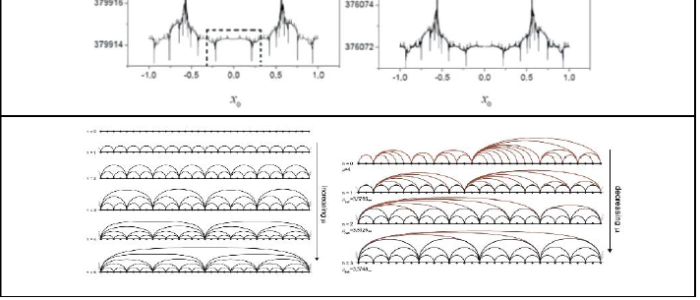
Finally, as we describe below in Part IV, recently we have made use of density functional theory, in the form of a discrete-time Landau equation, to link this subject to low-dimensional nonlinear dynamics, their RG fixed-point maps for the routes to chaos, and the understanding of the generalized statistical mechanics represented by the Tsallis entropy expression.