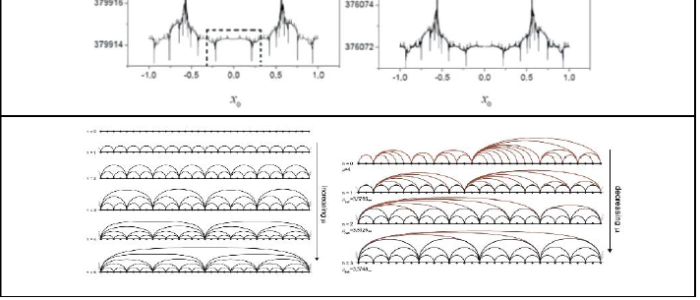
Random walk analogs. Elliot Montroll advanced a particularly efficient and elegant format to study random walks and renewal processes [8, 9]. The linearity property of independent identically distributed (iid) events (on regular lattices when spatial positions are required) allowed for a prominent role for the generating functions of the basic sets of probabilities. Once determined, Fourier, Laplace or z-transforms, their inverses, and use of differentiation when necessary, facilitates access to all conceivable properties [8, 9]. Recurrence relations are expressible as convolutions. First passage times become trapping events and traps can be arranged to form lines, surfaces, etc. Distinction between time and number of events along a sequence of steps leads to a fitting continuous time random walk description.
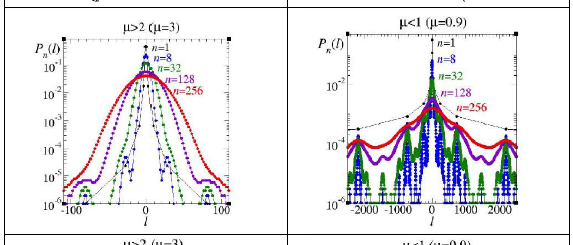
How to make use of these stochastic processes in other fields? First, we established analogies via the identification of convolutions present in the basic expressions. One case is the Ornstein-Zernicke relation, a common starting point for the development of integral equation approaches for correlation functions descriptive of equilibrium fluid structures. Another one is the Green function relation for tight binding electronic band structures. Secondly, there is the requirement for primary events in photosynthesis to be triggered, only after the trapping at a reaction site of more than one energy packet. This led to the study of first passage times for multiple walkers.The elegant Weierstrass walk, designed by Montroll and colleagues [10] to observe the emergence in the appropriate limits of either the Gaussian or the Levy distributions, has a rich set of scaling properties reminiscent of those of the nontrivial fixed points of the Renormalization Group (RG) when applied to critical phenomena in thermal systems. It was our interest to generalize this specific walk into an infinite family of them, that took the form of a universality class, to see if it revealed more features of this likeness, such as the flow to trivial fixed points. Moreover, it presented the opportunity of calculating entropies for the entire family of step distributions, and observe if the associated fixed points represent entropy extrema. In this way it was possible to reveal a hidden connection between the RG technique and entropy optimization [4].
How to make use of these stochastic processes in other fields? First, we established analogies via the identification of convolutions present in the basic expressions. One case is the Ornstein-Zernicke relation, a common starting point for the development of integral equation approaches for correlation functions descriptive of equilibrium fluid structures. Another one is the Green function relation for tight binding electronic band structures. Secondly, there is the requirement for primary events in photosynthesis to be triggered, only after the trapping at a reaction site of more than one energy packet. This led to the study of first passage times for multiple walkers.The elegant Weierstrass walk, designed by Montroll and colleagues [10] to observe the emergence in the appropriate limits of either the Gaussian or the Levy distributions, has a rich set of scaling properties reminiscent of those of the nontrivial fixed points of the Renormalization Group (RG) when applied to critical phenomena in thermal systems. It was our interest to generalize this specific walk into an infinite family of them, that took the form of a universality class, to see if it revealed more features of this likeness, such as the flow to trivial fixed points. Moreover, it presented the opportunity of calculating entropies for the entire family of step distributions, and observe if the associated fixed points represent entropy extrema. In this way it was possible to reveal a hidden connection between the RG technique and entropy optimization [4].